Previously, I've explained a simple ontological argument, and also a modal ontological argument. However, there's another modal ontological argument which interests me: That which was proposed by Kurt Gödel. It's Gödel's ontological argument!
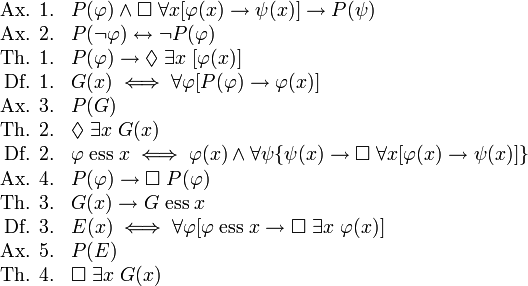 It's all so clear now! There must exist an x such that G(x)! (That is, God exists!)
It's all so clear now! There must exist an x such that G(x)! (That is, God exists!)What's that, you weren't convinced? Indeed, most skeptics would be unimpressed, since it looks so obscurantist. The argument seems to work solely on the principle of "blinded by Science!", or in this case, "blinded by Symbolic Logic!" Obviously, the proof doesn't really prove what it purports to prove, or the argument would be backed by philosophers everywhere. I certainly don't expect everyone to have the knowledge to be able to read the proof, much less pinpoint the precise location where it might go wrong.
However, as it happens, I had already taught myself a bit of modal logic, so I thought, why not try reading the proof, you know, for fun? I'm not going to go through it step by step (unless my readers really want me to), but instead, I'll outline the basic idea, and explain where I think a flaw is. [Update: By request, I went through the proof, step by step.]
The basic idea of Gödel's argument is based on the previous modal ontological argument. According to the modal ontological argument, God, by definition, necessarily exists. Therefore, if it's even possible that God exists, then God must exist in all possible worlds, including the one which we happen to live in. The problem is that we still have yet to show that God is possible.
And this is where Gödel comes in. Gödel supplies a proof of the fact that God is possible.
But first, we must define a "property". A property is an attribute of an object. For example, we might let "x" denote a particular apple, and "R" denote the property of being red. Thus R(x) is the statement "This apple is red." Gödel's central insight was to categorize some properties as "positive" and other properties as "not positive". We use P(R) to denote the statement "The property of being red is a positive property."
Gödel never tells us exactly what he means by "positive". That's because it doesn't really matter what exactly it means. The proof works, regardless. All that matters is that the positive properties obey a few axioms.
- Axiom 1: If property A is positive, and if property A entails property B, then B is positive.
- Axiom 2: If property A is positive, then the property not-A is not positive.
- Axiom 3: The property G is a positive property. (G is the property of being "God-like"; an object with property G has all positive properties)
- Axiom 4: If a property is positive, then it is positive in all possible worlds.
- Axiom 5: Necessary existence is a positive property.
Let's focus on axiom 1. What does it mean for property A to entail property B? That means that for every possible object in every possible world, if it has property A, then it also has property B. Of course, if there is not a single object in any of the possible worlds with property A, then A automatically entails B.
For example, let's consider the property of being an invisible pink unicorn, which we will call U. Let us presume that U is an impossible property. There is not a single object in any possible world which has the property U. Therefore, U entails O, which is the property of being omnipotent. I mean, have you met any invisible pink unicorns which are not omnipotent? I doubt it. Similarly, U entails every property. All of them, every single one. U entails the property of being solid dark blue, the property of being a flying spaghetti monster, and the property of not being a flying spaghetti monster.
So if U were a positive property, then every property would be positive. Obviously, this is not the case (see axiom 2). Therefore, U is not a positive property.
But this contradicts our intuition of what makes something positive (and recall that these axioms were based on intuition in the first place). Surely, there are some things which are positive, but sadly impossible. For instance, the invisible pink unicorn may be impossible, but if she existed, she would surely be a force for good. Wouldn't I be justified in saying that U is a positive property? No, because if I assume U is "positive", then I am essentially assuming that U is possible.
You might notice that in axiom 3, we assume G, the property of being God-like, is a positive property. Here, we're basically assuming that G is possible. Oops!
[An aside: In discussions of Gödel's modal ontological argument, people will inevitably start talking about Gödel himself. I haven't really seen any evidence that Gödel necessarily saw this argument as anything more than an interesting exercise in modal logic. Which is, of course, how I see it.]